EQUAÇÃO DE GRACELI.. PARA INTERAÇÕES DE ONDAS E INTERAÇÕES DAS FORÇAS FUNDAMENTAIS.
/
= [ ] ω , , / T] c [ [x,t] ] =
Em física teórica, a simetria conformal (ou simetria conforme) é uma simetria sob dilatação (invariância de escala[1]) e sob as transformações especiais conformes. Em conjunto com o grupo de Poincaré esses geram o grupo de simetria conformada.[2]
Transformação conforme
Simetria conformal sob a especial transformação conforme com as seguintes relações.
- / = [ ] ω , , / T] c [ [x,t] ] =
- / = [ ] ω , , / T] c [ [x,t] ] =
- / = [ ] ω , , / T] c [ [x,t] ] =
onde gera translações, gera transformações de escala como um escalar e gera as transformações conformes especiais como um vetor covariante [3] sob transformações de Lorentz.
Supercondutores ferromagnéticos são materiais que apresentam, de modo simultâneo e intrínseco, ferromagnetismo e supercondutividade. Entre eles, podem-se citar UGe2,[1] URhGe,[2] e UCoGe.[3] Evidência de supercondutividade ferromagnética também foi relatada para ZrZn2 em 2001, mas relatórios posteriores[4] questionam tais descobertas. Esses materiais exibem supercondutividade na proximidade de um ponto crítico quântico magnético.
A natureza do estado supercondutor em supercondutores ferromagnéticos está atualmente em debate. As primeiras investigações[5] estudaram a coexistência de supercondutividade de onda s convencional com ferromagnetismo itinerante. No entanto, o cenário de emparelhamento de spin tripleto logo ganhou vantagem.[6][7] Um modelo de campo médio para coexistência de emparelhamento de spin tripleto e ferromagnetismo foi desenvolvido em 2005.[8][9]
Esses modelos consideram a coexistência uniforme de ferromagnetismo e supercondutividade, ou seja, os mesmos elétrons sendo ferromagnéticos e supercondutores ao mesmo tempo. Os supercondutores com ordem magnética espiral ou helicoidal configuram outro cenário onde há uma interação entre as ordens magnética e supercondutora no mesmo materia. Exemplos deles incluem ErRh4B4 e HoMo6S8. Nesses casos, os parâmetros de ordem supercondutora e magnética se entrelaçam em um padrão espacialmente modulado, o que permite sua existência mútua, apesar de não ser mais uniforme. Mesmo o par spin singleto pode coexistir com o ferromagnetismo dessa maneira.
Teoria
Em supercondutores convencionais, os elétrons que constituem o par de Cooper têm spin oposto, formando os chamados pares de spin singletos. No entanto, outros tipos de emparelhamento também são permitidos pelo princípio de exclusão de Pauli. Na presença de um campo magnético, os spins tendem a se alinhar com o campo, o que significa que um campo magnético é prejudicial para a existência de pares de Cooper no estado singleto. Um hamiltoniano de campo médio viável para modelar ferromagnetismo itinerante coexistindo com um estado tripleto de de spin não unitário pode, após a diagonalização, ser escrito como:[8][9]
,/ = [ ] ω , , / T] c [ [x,t] ] =
,/ = [ ] ω , , / T] c [ [x,t] ] =
./ = [ ] ω , , / T] c [ [x,t] ] =
Classes cristalinas piroelétricas
As estruturas cristalinas podem ser divididas em 32 classes, ou grupos pontuais, segundo o número de eixos rotacionais e planos de reflexão que exibem e que mantém a estrutura do cristal piroelétrico. Entre as 32 classes de cristais, vinte e uma são não-centrossimétricas (não têm centro de simetria). Destas vinte e uma, vinte exibem piezoeletricidade direta, sendo a restante a classe cúbica 432. Dez destas vinte classes piezoelétricas são polares, i.e., exibem uma polarização espontânea, tendo um dipolo na sua célula unitária, e exibem piroeletricidade. Todos os cristais polares são piroelétricos.
Classes de cristal piezoelétricas: 1, 2, m, 222, mm2, 4, -4, 422, 4mm, -42m, 3, 32, 3m, 6, -6, 622, 6mm, -62m, 23, -43m
Piroelétricas: 1, 2, m, mm2, 3, 3m, 4, 4mm, 6, 6mm
Desenvolvimentos recentes
Têm sido feitos progressos na criação de materiais piroelétricos artificiais, usualmente na forma de uma película fina, a partir de nitreto de gálio (GaN), nitrato de césio (CsNO3), fluoretos de polivinila, derivados de fenilpirazina, e ftalocianina de cobalto (ver cristal piroelétrico). O tantalato de lítio (LiTaO3) é um cristal que exibe tanto propriedades piezoelétricas como piroelétricas que tem sido usado para criar fusão nuclear em pequena escala ("fusão piroelétrica").[2]
Descrição matemática
O coeficiente piroelétrico pode ser descrito como a variação do vetor de polarização espontânea com a temperatura[3]:
- / = [ ] ω , , / T] c [ [x,t] ] =
em que pi (Cm-2K-1) é o vetor do coeficiente piroelétrico.
Geração de energia
Um material piroelétrico pode ser repetidamente aquecido e arrefecido (de forma análoga a uma máquina térmica) para gerar energia elétrica utilizável. Um grupo calculou que a piroeletricidade num ciclo de Ericsson poderia atingir uma eficiência de Carnot igual a 50%,[4] enquanto um outro estudo descobriu um material que poderia em teoria atingir uma eficiência de 84 a 92%[5] (estes valores de eficiências são para a piroeletricidade propriamente dita, ignorando perdas no aquecimento e arrefecimento do substrato, outras perdas por transferência de calor, e todas as restantes perdas noutras partes do sistema). Entre as possíveis vantagens dos geradores piroelétricos na geração de eletricidade (quando comparada com o motor convencional mais gerador elétrico), incluem temperaturas de funcionamento potencialmente menores, equipamento menos volumoso, e menos partes móveis.[6] Embora tenham sido aceitas algumas patentes para um tal aparelho,[7] a sua comercialização não parece estar próxima.
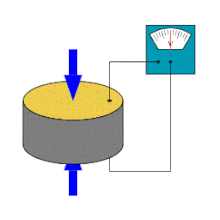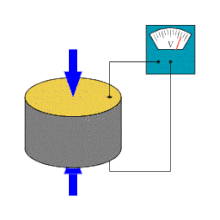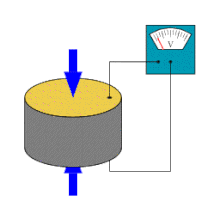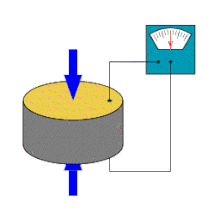
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.
Mecanismo
O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).
O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.[1]
Cristais
Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.
Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.
Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.
A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.[2]
Descrição matemática
A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:[3]
Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinal aplicada.
Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.
Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:
Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.
A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que e . Assim, temos
onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.
Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.
Num material piezoelétrico também interessam os seguintes coeficientes:
- Coeficiente de acoplamento eletro-mecânico:
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.
- Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:
/ = [ ] ω , , / T] c [ [x,t] ] =

 =
=







![{\displaystyle [P_{\mu },P_{\nu }]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/962f89d6eb3cb638b9c32374b3e8de33de9f9893)
![{\displaystyle [D,K_{\mu }]=-K_{\mu },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6302195130d18df1a27264b3cd8ce7b8d833cd26)
![{\displaystyle [D,P_{\mu }]=P_{\mu },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab61651b659463ad283cbf2e14da8e6ef6db2018)
![{\displaystyle [K_{\mu },K_{\nu }]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce875fa88d23d9d013448208a83cb080b670a494)
![{\displaystyle [K_{\mu },P_{\nu }]=\eta _{\mu \nu }D-iM_{\mu \nu },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd750795f2789414837b421ae2c8f3bc458bb4a)















Comentários
Postar um comentário